The dynamic nature of mathematics

Professor Aidan Sims and Associate Professor David Pask will collaborate on the ARC Discovery Project with experts from the University of Sydney and the University of Durham in the UK – Chief Investigators Professor Jacqui Ramagge and Dr Nathan Brownlowe – and Partner Investigator A/Prof Lisa Clark from the Victoria University of Wellington in New Zealand.

Dynamic systems

Each investigator has extensive knowledge in fields relevant to the project, particularly dynamic systems (which describe and model how complicated systems evolve with time and are central to modern mathematics and its applications), algebras (mathematical structures consisting of elements that can be added, multiplied and scaled by constants) and groupoids.

Groupoids are a more recent development in the world of mathematics that is generating substantial interest as a facilitator of two-way paths (or dualities) between operator algebra and dynamic systems.

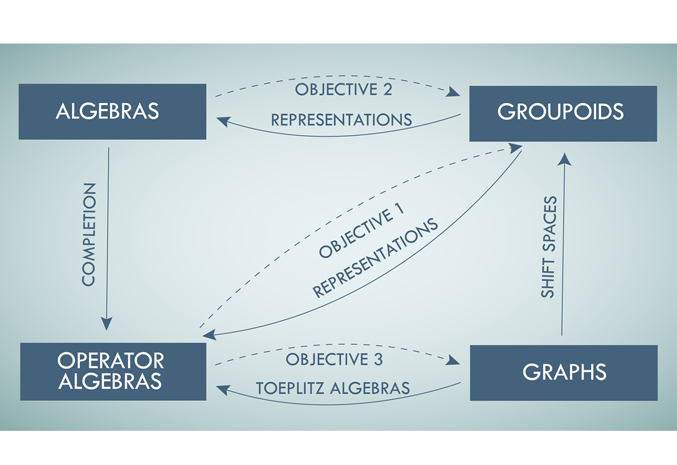
Image: The objectives of this project, pictured above, comprise an ambitious and timely program to build upon the newly available reconstruction machinery to obtain full duality between groupoids and both operator algebras and abstract algebras, and to reconstruct very general analogues of directed graphs from algebraic data and connect these results.

Prof Sims explains: “In mathematics, dualities allow us to translate questions from one context to another in which they are easier to solve and then translate the answer back again.

“You can think of it as though you were gazing at an immensely complicated machine, and were asked to write down what you saw, so you could analyse how it worked later.

“You might take a whole lot of measurements and draw some diagrams, and get an idea of the overall workings of the machine, but you wouldn’t be able to go back and reconstruct exactly the same machine with exactly the same internal workings just from what you were able to write down.

“By changing the way we think of representing a dynamical system with algebras or operator algebras, we can actually see every nuance of the dynamical system encoded in the operator algebra. It’s like we’ve found a way of recording every detail of the machine so that we could rebuild it exactly as we have seen it, just from the collection of technical specifications we’ve been able to capture on paper.”

A beautiful puzzle

The long-term commercial impact of fundamental research in mathematics is common but is often hard to predict as it typically arises through the development of new technologies based on the use of mathematical concepts in other disciplines.

“The way Boolean algebra was developed almost 100 years before the invention of computers, which could never have been dreamt of without it,” Prof Sims explains.

“When matrices and the Perron-Frobenius theorem were developed they seemed purely theoretical, but the Google search engine would never have existed if the theorem hadn’t been uncovered. “And the whole of modern medicine – the scientific development, testing and evaluation of medicines and medical procedures – owes its existence to Thomas Bayes’ work on the foundations of what we now know as statistics.”

When asked why he loves mathematics and what keeps him striving for answers to questions which sometimes have an ambiguous outcome, Prof Sims replied: “As a society, we have built up a perception of mathematics as being abstract, and difficult. But that’s no more or less true of mathematics than it is of music or art or history or medicine or fitting and machining or any number of other areas of expertise.

“There are no limits on how creative you can be in developing an out-of-left-field approach to a problem, and there is such a huge sense of achievement when you make a breakthrough.

“I love the collaborative nature of mathematical research – I’m in the incredibly fortunate position of being paid to collaborate with friends from around the globe on the world’s most intricate puzzle game. And yet at the same time, I know that every puzzle we solve could be the key to some technological breakthrough in the future.”